线性代数在微观世界中的应用张朝阳的物理课解析矩阵对角化

在探索微观世界的奥秘时，物理学家们经常依赖于线性代数这一强大的数学工具。线性代数不仅在宏观世界的物理学中扮演着关键角色，而且在描述微观粒子的行为和相互作用时也至关重要。《张朝阳的物理课》深入探讨了如何利用线性代数中的矩阵对角化技术来解决量子力学中的问题，本文将详细介绍这一过程及其在微观世界中的应用。

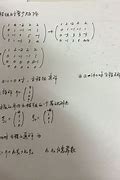
线性代数与微观世界

线性代数是研究向量空间和线性映射的数学分支，它通过矩阵和向量的语言，提供了一种简洁而强大的方式来描述和解决线性问题。在微观世界中，量子力学的基本原理要求我们使用波函数来描述粒子的状态，而这些波函数通常可以用向量表示。量子力学中的算符，如动量、位置和能量算符，可以用矩阵来表示。因此，线性代数成为了连接数学与物理的桥梁，帮助我们理解和预测微观粒子的行为。

矩阵对角化的重要性

矩阵对角化是线性代数中的一个核心概念，它涉及到将一个矩阵变换为一个对角矩阵，即只有主对角线上有非零元素的矩阵。对角矩阵的一个重要特性是它的幂运算非常简单，这使得对角化在求解线性系统的动态行为时非常有用。在量子力学中，矩阵对角化可以帮助我们找到系统的本征态和本征值，即粒子的可能状态和相应的能量。

《张朝阳的物理课》中的矩阵对角化

在《张朝阳的物理课》中，张朝阳教授通过具体的例子展示了如何应用矩阵对角化来解决量子力学问题。他首先介绍了矩阵的本征值和本征向量的概念，然后说明了如何通过相似变换将矩阵对角化。通过对角化，我们可以得到系统的能量本征值和相应的本征态，这对于理解量子系统的能级结构至关重要。

应用实例：量子谐振子

一个经典的例子是量子谐振子的能级问题。在量子力学中，谐振子模型描述了粒子在一维势场中的振动。通过将谐振子的哈密顿算符（能量算符）矩阵化，并对其进行对角化，我们可以得到谐振子的能级和波函数。这些结果不仅揭示了谐振子的量子特性，如能级的离散性和零点能的存在，而且还为理解更复杂的量子系统提供了基础。

结论

线性代数中的矩阵对角化技术是理解微观世界的关键工具。通过《张朝阳的物理课》的讲解，我们不仅学习了如何将这一数学工具应用于量子力学问题，而且还体会到了数学与物理之间的深刻联系。在未来的科学探索中，线性代数将继续作为我们理解自然界的基础语言，帮助我们揭开更多微观世界的秘密。